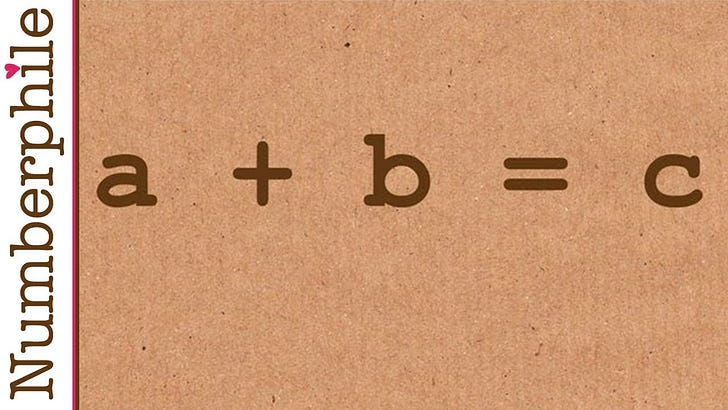🧮 Math on Mondays: 🤯 When Daydreaming Leads to Mathematical Breakthroughs
🦸♂️➗ Accidental Hero Solves Math Mystery That Stumped Giants 🤯🧮 When Daydreaming Leads to Mathematical Breakthroughs
😽 Keepin’ It Simple Summary for Younger Readers
👧🏾✊🏾👦🏾
🧠🔢 Imagine a super tricky math problem that stumped even the smartest people for over 100 years! It's about a special pattern in numbers that kept hiding its secrets. Then, one day, a mathematician who was supposed to be writing a test started doodling instead. Surprisingly, his doodles led him to crack part of this big mystery! This shows that sometimes, letting your mind wander can lead to amazing discoveries. Who knows? Maybe your next daydream could solve an ancient puzzle too! 🌟💡
🗝️ Takeaways
🎭 Mathematics can be as dramatic as a telenovela
🦋 Small doodles can lead to huge breakthroughs
🏋️♂️ Even "simple" math problems can challenge experts for decades
🌈 Creativity and unconventional thinking are crucial in mathematics
🤝 Math progress often comes from building on others' work
🔍 Verifying complex proofs is a major challenge in modern mathematics
🔢🧮 From Procrastination to Revelation: A Math Odyssey a Century in the Making 🕰️🤯
In the labyrinthine world of mathematics, where abstract concepts dance with real-world implications, a seemingly innocuous sequence of numbers has been taunting the brightest minds for over a century. But sometimes, breakthrough moments come when we least expect them - like when we're avoiding writing a final exam.
The Sequence That Stumped Giants 🧠💭
Picture this: 2, 5, 10, 17, 26... Looks simple, right? This sequence, formed by
has been the mathematical equivalent of a siren's call, luring number theorists to dash their ships of certainty upon the rocks of complexity.
A Century of Head-Scratching 🤔💡
1898: Carl Størmer proves these numbers' largest prime factors approach infinity. (Cue dramatic music)
Mid-1930s: Sarvadaman Chowla and Kurt Mahler independently show the lower bound is about log(log n). (Mathematicians everywhere: "That's it?")
For decades: Crickets chirp as progress stalls. Mathematicians suspect there's more but can't prove it.
“It doesn’t take far to get to the boundary of our knowledge,” said Andrew Granville of the University of Montreal.
Enter the Accidental Hero: Hector Pasten 🦸♂️📚
Picture a Chilean mathematician, Hector Pasten, sitting at his desk, supposed to be writing a final exam. Instead, he's doodling numbers, his mind wandering to this century-old problem. Little did he know that procrastination was about to become his superpower.
Pasten's Eureka Moment 💡🎉
He creates a funky elliptic curve:
\(y^2 = x^3 + 3x + 2n\)(Math nerds, contain your excitement!)
Applies some mind-bending theory involving Shimura curves. (Non-math folks, just nod and smile)
Combines this with some old-school transcendence theory.
Boom! Proves the largest prime factor must be at least about (log(log n))^2.
Why Should You Care? (Besides Impressing at Parties) 🍸🧐
The ABC Conjecture: Pasten's work might help crack one of math's most controversial problems. It's like the mathematical equivalent of solving a celebrity scandal.
New Mathematical Swiss Army Knife: His techniques could be applied to other sequences, potentially unleashing a tsunami of new discoveries.
Philosophy of Discovery: Sometimes, the biggest breakthroughs happen when we're not looking for them. So, next time your boss catches you daydreaming, just say you're following in Pasten's footsteps!
The Human Side of Numbers 👨🔬❤️🔢
This isn't just about cold, hard numbers. It's a story of human perseverance, the thrill of discovery, and the beauty of the unexpected. Pasten's breakthrough reminds us that even in the most abstract realms of thought, there's room for serendipity and human touch.
As we continue to peel back the layers of mathematical mystery, who knows what other mind-bending discoveries await? Maybe the next great math breakthrough is hiding in your doodles during a boring meeting. So keep scribbling - you never know when you might accidentally revolutionize mathematics!
Part II - Not easy as ABC, or is it?
🧮 Clash of the Math Titans: The ABC Conjecture Showdown 🤯
A storm has been brewing for nearly a decade in the rarefied air of high-level mathematics. Picture this: a lone mathematical maverick claims to have solved one of the field's most notorious puzzles, only to face a wall of skepticism from his peers. No, this isn't the plot of a cerebral thriller—it's the real-life drama surrounding the abc conjecture proof. Grab your popcorn (or perhaps a graphing calculator), because this story has more twists and turns than a Klein bottle!
The Riddle That Stumped the Smartest 🧩
Before we dive into the controversy, let's talk about the star of our show: the ABC conjecture. Don't let the simple name fool you—this mathematical beast has been giving number theorists nightmares for decades.
Imagine you have three positive integers: a, b, and c. They play nice and follow the rule a + b = c. Oh, and just to keep things spicy, they don't share any prime factors. Now, multiply all the prime factors of a, b, and c together. The abc conjecture essentially says, "Hey, that product is usually going to be way bigger than c."
Sounds simple, right? Well, if you think that, I've got a bridge in a non-Euclidean space to sell you. This little conjecture has its tentacles in so many areas of mathematics that proving it would be like finding the Holy Grail, the Philosopher's Stone, and the last digit of pi all rolled into one.
Enter the Mathematical Wizard 🧙♂️
In 2012, a mathematical sorcerer named Shinichi Mochizuki emerged from his tower at Kyoto University, brandishing a 500-page spell—er, proof. Mochizuki wasn't just any mathematician; he was already famous for conjuring up mind-bending ideas in the arcane art of anabelian geometry.
His proof of the abc conjecture came wrapped in a shiny new package he called "Inter-universal Teichmüller Theory" (IUT). Imagine trying to explain quantum physics using interpretive dance, and you'll get an idea of how comprehensible most mathematicians found Mochizuki's work.
The Fog of Math War ☁️🔢
As the mathematical community dove into Mochizuki's papers, confusion reigned supreme. Definitions sprawled over pages like kudzu, while theorem proofs basically said, "Trust me, it works." Even the brightest minds in the field felt like they were trying to read a book written in invisible ink.
Workshops were held, papers were scrutinized, and yet clarity remained as elusive as a rational solution to
(That's a little Fermat's Last Theorem humor for you. We mathematicians are a wild bunch!)
The Plot Thickens: Enter the Skeptics 🕵️♂️🕵️♀️
Just when it seemed the mathematical world might be forever divided into "Those Who Claim to Understand Mochizuki" and "The Rest of Us," two daring heroes emerged from the mists of academia. Peter Scholze (with his trusty Fields Medal) and Jakob Stix decided to beard the lion in his den.
These intrepid mathematicians journeyed to Kyoto for a mathematical showdown with Mochizuki himself. After intense discussions that probably made Good Will Hunting look like a preschool counting lesson, Scholze and Stix emerged with a bombshell: they claimed to have found a "serious, unfixable gap" in the proof.
The problem? Something about "measuring sticks" behaving oddly when taken for a walk around a mathematical merry-go-round. (If that doesn't make sense to you, congratulations! You're on par with most of the world's top mathematicians.)
Mochizuki Strikes Back 🥋
Did our Japanese genius take this lying down? Of course not! Mochizuki fired back, essentially saying Scholze and Stix had mistaken mathematical apples for oranges.
According to him, they just needed to meditate on his ideas for a few more years (or decades) to see the light.
Where We Stand: Mathematical Mayhem 🌪️
So here we are, stuck in a mathematical Mexican standoff. On one side, Mochizuki and his followers claim to have slain the ABC dragon. On the other, most of the mathematical community scratches their heads and wonders if they've collectively forgotten how to count.
This isn't just academic squabbling over who gets the last donut at the department meeting. The ABC conjecture is a big deal, with tendrils reaching into many areas of mathematics. Resolving this could unlock doors we didn't even know existed in the mathematical universe.
What's Next in This Number-Crunching Saga? 🔮
As the dust settles (or rather, as the chalk dust continues to swirl), a few things are clear:
The ABC Conjecture isn't going anywhere. Like that one weird uncle at family gatherings, it'll keep popping up until someone finally deals with it.
Mathematicians are having to rethink how they verify proofs. When your proof is longer than "War and Peace" and about as easy to understand, traditional peer review starts to look a bit shaky.
Even if Mochizuki's proof turns out to be a beautiful mirage, the journey may have led us to mathematical oases we never knew existed.
This whole saga proves that mathematics, far from being a dry, dusty subject, can have all the drama, passion, and plot twists of a telenovela. Just with more Greek letters.
As we wait for the next act in this mathematical opera, one thing's for sure: the ABC conjecture continues to add spice to the world of number theory. Who knows? The resolution might come from an unexpected quarter. So keep your eyes peeled and your calculators ready—the next big breakthrough could be just a quadratic equation away!